A Gentle Introduction to Forecasting in Merlion

We begin by importing Merlion’s TimeSeries class and the data loader for the M4 dataset. We can then divide a specific time series from this dataset into training and testing splits.

from merlion.utils import TimeSeries
from ts_datasets.forecast import M4

time_series, metadata = M4(subset="Hourly")[0]
train_data = TimeSeries.from_pd(time_series[metadata.trainval])
test_data = TimeSeries.from_pd(time_series[~metadata.trainval])

We can then initialize and train Merlion’s DefaultForecaster, which is an forecasting model that balances performance with efficiency. We also obtain its predictions on the test split.

from merlion.models.defaults import DefaultForecasterConfig, DefaultForecaster
model = DefaultForecaster(DefaultForecasterConfig())
model.train(train_data=train_data)
test_pred, test_err = model.forecast(time_stamps=test_data.time_stamps)

Inferred granularity <Hour>
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/statsmodels/base/model.py:604: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/statsmodels/base/model.py:604: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "
/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/statsmodels/base/model.py:604: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "

Next, we visualize the model’s predictions.

import matplotlib.pyplot as plt
fig, ax = model.plot_forecast(time_series=test_data, plot_forecast_uncertainty=True)
plt.show()

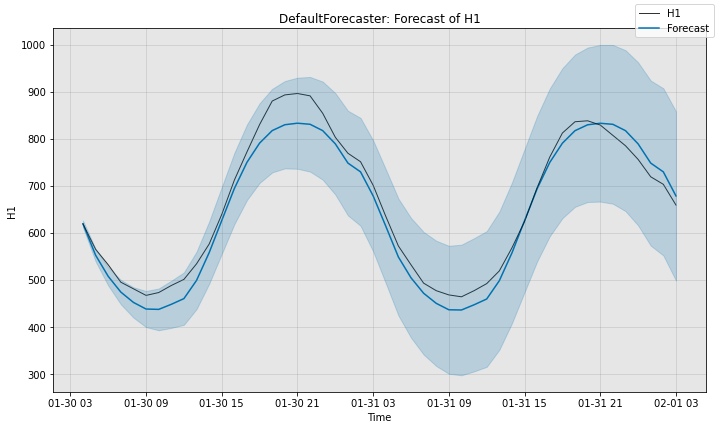
Finally, we quantitatively evaluate the model. sMAPE measures the error of the prediction on a scale of 0 to 100 (lower is better), while MSIS evaluates the quality of the 95% confidence band on a scale of 0 to 100 (lower is better).

from scipy.stats import norm
from merlion.evaluate.forecast import ForecastMetric

# Compute the sMAPE of the predictions (0 to 100, smaller is better)
smape = ForecastMetric.sMAPE.value(ground_truth=test_data, predict=test_pred)

# Compute the MSIS of the model's 95% confidence interval (0 to 100, smaller is better)
lb = TimeSeries.from_pd(test_pred.to_pd() + norm.ppf(0.025) * test_err.to_pd().values)
ub = TimeSeries.from_pd(test_pred.to_pd() + norm.ppf(0.975) * test_err.to_pd().values)
msis = ForecastMetric.MSIS.value(ground_truth=test_data, predict=test_pred,
                                 insample=train_data, lb=lb, ub=ub)
print(f"sMAPE: {smape:.4f}, MSIS: {msis:.4f}")

sMAPE: 4.1944, MSIS: 18.9331